4/22/18 · Issuu is a digital publishing platform that makes it simple to publish magazines, catalogs, newspapers, books, and more online Easily share your publications and getVeja grátis o arquivo Howard, Anton Calculo Um Novo Horizonte Exercícios resolvidos capitulo 15 enviado para a disciplina de Cálculo III Categoria Outro 2For ∫cos2 3θdθ For a correct integral expression including limits (may be implied 6 9 14 0 (1 )( 7 ) 2(2 4) 3(2 2) 0 3 2 2 Correct shape for π θ π 2 1 2 −1 < < including maximum in 1st quadrant Correct form at O and no extra sections (ii) 3 Area is

Calculus Set Free Infinitesimals To The Rescue Volume 3 Spring 21 Preliminary Edition By Bryan Dawson Issuu
π/2 9 cos 2(θ) dθ 0
π/2 9 cos 2(θ) dθ 0-Anuncio 3 r2 = 9 sin 2θ, r ≥ 0, 0 ≤ θ ≤ π/2 ∫ π 2 1 · 9 sin 2θdθ Area = 0 2 π 2 9 = − cos 2θ 4 0 9 = 2 4 r = tan θ, π/6 ≤ θ ≤ π/3 ∫ π 3 1 Area = tan2 θdθ π 2 6∫ π 1 3 = sec2 θ − 1dθ 2 π6 1 √ 1 π π = ( 3− √ − ) 2 6 3 3 1√ 1 3− π = 3 12 11 r = 3 2 cos θ ∫ 1 π Area = 2 · (3 2 cos θ)2 dθ 2 0 ∫ π = 9 12 cos θ 4 cos2 θdθ 0 = 11π 23 ∫ π 3µ 2 k " 1/ 2 $ kτ 4 π2µ % 1/2!π 4 " = τ 4 √ 2 as advertised Problem 36 (a) Show that if a particle describes a circular orbit under the influence of an attractive central force directed at a point on the circle, then the force varies as the



Weierstrass Substitution Wikipedia
$\begingroup$ $9\sin^2 \theta1=0$ gives $\sin \theta=\pm \frac13$ so there are in fact 3 solutions $\endgroup$ – rae306 Aug 2 '15 at $\begingroup$ The sine is $\pm \frac{1}{3}$ The domain of the trig functions has not been specified, so there are infinitely many answers, tough to do a commaseparated list $\endgroup$ – AndréRπ/4 0 35cos2θ cos2θ dθ = Rπ/4 0 3 cos2θ 5cos2θ cos2θ dθ = Rπ/4 0 (3sec2θ 5)dθ =3tanθ 5θπ/4 0 = 3tanπ 4 5π 4 −(00)=35π 4I Limits in θ θ ∈ 0π;
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history7/24/14 · Solución Por simetría, se calculará 4 veces el área de la porción en el primer cuadrante cos 2θ = 0 ⇒ θ = π 4 , en el primer cuadrante A = 4 ⋅ ∫0 π 4 1 2 r2 dθ = 2∫0 π 4 r2 dθ = 2∫0 π 4 9cos 2θ dθ A = 18∫0 π 4 cos 2θ dθ = 9 Área en coordenadas polares 5Evaluate The Integral π/2 3 Cos2θ Dθ 0 ;
I Limits in φ φ ∈ 0,π/2;4/13/19 · 0 # 0 π/2 sin2 xdx =!(c) Determine whether the imroper integral R ?



Solved Example 3 Find Dx Solution Let X 2 Tan 8 Z 2 8 Chegg Com


Osa Theoretical Generation Of Arbitrarily Homogeneously 3d Spin Orientated Optical Needles And Chains
Sin3 x cos xdx =?5/31/10 · Writeacher May 31, 10 When the sin/cos are in odd powers, use the substitution cosθdθ=d (sinθ), or sinθdθ=d (cosθ) ∫sin³θcos³θd&theta (from 0 to π/2) =∫sin³θ (1sin²θ) (cosθdθ) =∫ (sin³θsin 5 θ) (d (sinθ)) (from 0 to sin (π/2)) = sin 4 θ/4sin 6 θ/6 (from 0 to 1)11/3/12 · ASTM002 Galaxies Lecture notes 06 (QMUL),



Math 101 Homework 5 Solutions Outside Of The Circle X


Evaluate The Following Definite Integral Cos8 Sin 3 8 D8 For 8 0 P 2 Sarthaks Econnect Largest Online Education Community
See the answer Evaluate the integral π/2 3 cos 2 θ dθ 0 Videos Stepbystep answer 0150 0 0 Expert Answer 100% (63 ratings) Previous question Nextπ/2 cosn (x)dx = 1 n−1( x)sin( π/2 n − 1 π/2 cosn−1(x )dx 0 n 0 n 0 Observe nthat cos −1(x) sin(x)π/2 is zero for n ≥ 2 Let us call 0 π/2 A n = ncos (x)dx 0 Combined with this observation, the recursion formula of (i) gives A n = n − 1 A n−2, n ≥ 2 n = 1 n = 1 (6) = π/2 n = 0 Here the values have been found directly for n = 0 and n = 1π 2 −π 2 dθ acosθ 0 rdr= π 2 −π 2 1 2 r2 acosθ 0 dθ = a2 2 π 2 −π 2 cos2 θdθ= a2 2 π 2 −π 2 cos2θ1 2 dθ = π 4 a2 (2) 積分の順序を変更して計算すると, 2 1 dx 2 1 x yexy dy = 1 1 2 dy 2 1 y yexy dx 2 1 dy 2 1 yexy dx = 1 1 2 exy 2 1 y dy 2 1 exy 2 dy = 1 1 2 (e2y − e) 1 = ( 解答



Math Polar Coordinates Ppt Download



Show That Int 0 Pi 2 Sin P Theta Cos Q Theta D Theta Frac Sqrt Frac P 1 2 Sqrt Frac Q 1 2 2 Sqrt Frac P Q 2 2 P Q 1 Mathematics Stack Exchange
Evaluate the integralπ/47 9 cos2 (θ)cos2 (θ) dθ Evaluate the integralπ/47 9 cos2 (θ)cos2 (θ) dθ Watch laterUse a graphing utility to graph three solutions, one of which passes through the given point ds/dθ = tan 2θ, (0, 2)3 4), (3 4,´ 3?



Find The Integral Of Math Int 0 Pi 2 Frac Dx 4 Cos 2x 9 Sin 2x Math Quora



Solved Evaluate The Integral Integral 0 To Pi 2 7 Cos 2 Chegg Com
(b) Evaluate the integral R 2x 2x2?5x?3 =?(1 − cos2 = 9 2 θ− 1 2 sen 2θ π/2 π/4 = 9 8 (π 2) 8 A = 3 π/2 π/2 1 2 θ 2 dθ = 1 10 θ5 3 /2 /2 = 121 160 π5 9 4 A = π 0 1 2 (5sen θ)2 dθ = 25 4 π 0 (1 − cos2 θ) dθ = 25θ− 1 2 sen 2θ π 0 = 4 π 10 2 A = 2 π/2 −π/2 1 2 (4 − senθ) 2 dθ = π/2 −π/2 16 − 8senθ sen2 θ dθ = π/2 −π/2 16 sen2 θ dθ pelo Teorema 557(b) = 2 π/2 0 16 sen2 θ dθ pelo Teorema 557(a) = 2 π/2 0 16 1 2 (1 − cos2 θ) dθ0 cos2 θ dθ = 0 1 2 (1 cos 2θ) dθ halfangle identity 1 £ 1 ¤π/2 £¡ ¢ ¤ = 2 θ 2 sin 2θ 0 = 12 π2 0 − (0 0) = π 4 Rπ Rπ£ ¤2 Rπ£ ¤2 Rπ 9



Fp3 Chapter 4 Integration Ppt Download



Unit 4 Applications Of Integration
∫ π/2 0 sin 3 θ cos 2 θ dθ Students also viewed these Mathematics questions A) Evaluate the integral R ?JEE Main If ∫ (dθ/cos2 θ(tan 2θsec 2θ))= λ tanθ2 logef (θ)C where C is a constant of integration, then the ordered pair (λ, f (θSolution The full length of the cardioid is given by the parameter interval 0 ≤ θ ≤ 2π, so Formula 5 gives s 2 Z 2π Z 2π q dr L= r2 dθ = (1 − cos θ)2 sin2 θdθ 0 dθ 0 Z 2π p = 1 − 2 cos θ cos2 θ sin2 θdθ 0 2π √ Z = 2 − 2 cos θdθ 0 r 2π θ Z = 4 sin2 dθ 0 2 Z 2π θ = 2 sin dθ 0 2 Z 2π θ = 2 sin dθ 0 2



Interference Contrast Optical Activity A New Technique For Probing The Chirality Of Anisotropic Samples And More Royal Society Open Science



Introduction To Trigonometric Substitution Video Khan Academy
Cos4θ)dθ = 81 4 3 2 θ sin2θ 1 8 sin4θ π/3 π/4 = 81 4 h π 2 √ 3 2 − √ 16 − 3π 8 10 i = 81 4Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorEvaluate each definite integral in Problems 15 Use Table II on pages to find the and derivative View Answer



Trigonometric Substitution Wikipedia



Interference Contrast Optical Activity A New Technique For Probing The Chirality Of Anisotropic Samples And More Royal Society Open Science
12/9/ · = 2 – 6 sin 2 θ cos 2 θ –3 6 sin 2 θ cos 2 θ 1 = 0 = RHS (ii) We have, LHS = (sin 8 θ – cos 8 θ) = (sin 4 θ) 2 – (cos 4 θ) 2 = (sin 4 θ – cos 4 θ) (sin 4 θ cos 4 θ) = (sin 2 θ – cos 2 θ) (sin 2 θ cos 2 θ) (sin 4 θ cos 4 θ) = (sin 2 θ – cos 2 θ){(sin 2 θ) 2 (cos 2 θ) 2 2 sin 2 θ cos 2 θ – 2 sin 2 θ cos 2 θ4 Abstract and Applied Analysis In this study, our goal is to prove dh(r)/dr0Sincein(25), both g(r)and var(cos2θ)/cos2θ2 are always positive, to achieve our goal, we only need to prove the two theorems below Theorem 21 Q 1(r)≡g(r)−1−2g(r)cos2θ2 0 (26) Theorem 22 Q 2(r)≡var(cos2θ)−1cos2θ 0 (27) Remark 23(3) Identify the curve marked by ‹ on the θrplane for 0 ď θ ď 2π (4) Find the area of the shaded region Solution (1) Let 1cosθ = 3cosθ Then 2cosθ = 1 or θ = π 3, 5π 3 From the figure, it is also clear that C1 and C2 intersection at the origin Therefore, the points of intersections are (3 4, 3?



Evaluate The Integral P 47 9 Cos2 8 Cos2 8 D8 Youtube



Integral Evaluation Mathematics Statistics And Calculus Solution Manual Docsity
4/30/ · Free Online Scientific Notation Calculator Solve advanced problems in Physics, Mathematics and Engineering Math Expression Renderer, Plots, Unit Converter, Equation Solver, Complex Numbers, Calculation Historyµ 2 k " 1/2 r3/2 0 π 4 Now plugging in (5), we obtain ∆t =!Veja grátis o arquivo Resolução Griffiths MECANICA QUANTICA enviado para a disciplina de Mecânica Quântica Categoria Outro 2



Ex 7 11 14 Using Properties Evaluate Integral Cos5 X Dx



Complex Numbers Trig Identities Ppt Download
= acos2 θ − asin2 θ = acos2θ = 0 at θ = π 4, so the tangent here is vertical Similarly, for the second circle r = acosθ, dy dθ = acos2θ = 0 and dx dθ = −asin2θ = −a at θ = π 4, so the tangent is horizontal, and again the tangents are perpendicular 72 r = √ 1−08sin2 θ The parameter interval is 05/2/14 · Evaluate I = 0∫π cos4 x dx b Evaluate I = 0∫2π sin8 dx Solution a I = 0∫π cos4 x = 2 0∫π/2 cos4 x = 2 (1/2) B (1/2 , 5/2 ) = 3π / 8 b I = I = 0∫π sin8 x = 4 0∫π/2 sin8 x = 4 (1/2) B (9/2 , 1/2 ) = 35π / 64 13 14 Details I Example(1) Evaluate I = 0∫∞ x 6 e 2x dx x = y/2 x 6 = y 6 /64 dx = (1/2)dy x 6 e 2x dxSEÇÃO 102 CÁLCULO COM CURVAS PARAMETRIZADAS 5 x25 t=3 t− 3, y 2,0 ≤ 2 dx dt 2 dy dt 2 = 3 − 3t2 2 (6t) = 9 1 2t 2 t4 = 3 1 t 2 L = 2 0 3 1 t2 dt = 3t t3 = 14 26 x = 2 − 3s en2 θ, y = cos2 ,0 ≤ π 2 (dx/dθ)2 (dy/dθ)2 = (−6sen θcosθ)2 (−2sen 2θ)2= (−3sen 2θ)2 (−2sen2θ)2 = 13 sen2 2θ L = π/2 0 13 sen 2θdθ = − 13 2 cos2 θ π/2 0 =− 13 2



Resposta Do Capitulo 15


Pdf Trigonometric Integrals Jerome Delen Academia Edu
9/22/ · If cosθ = 12 13, 0 < θ < π 2, find the value of sin2 θ – cos2 θ 2 sin θ cos θ , 1 tan2 θ3 4), (0,0) (2) C2 can be parametrized by ␣Question Evaluate The Integral π/2 9 Cos2(θ) Dθ 0 This problem has been solved!


Solved 1 Evaluate The Iterated Integral P 4 0 Cos 8 5 Chegg Com


2 3 Trigonometric Substitutions Mathematics Libretexts
For simplicity, we assume that m(θ,t) has a periodic boundary condition (−π/2 ≤ θ ≤ π/2), and the connections of each neuron are limited to this periodic range θ0 is a stimulus feature to be detected, and the afferent input, h ext(θ,t), has its maximal amplitude c(t) at θ = θ0 We assume a static visual stimulus so that θ0 is2/11/15 · Evaluate the integral sin^7 θ cos^5 θ dθ 0, pi/2?27 π 2 sen3 θdθv 9 π 2 senθ sen2 θdθ v 9 π 2 senθ 1 cos2 θ dθ v 9 π 2 senθ from IT 101 WORD 1 at University of Technology and Life Sciences in



Fp2 Chapter 7 Polar Coordinates Ppt Download



Chapter 5
2 (x 1)e ?112xdx is convergent or divergent View AnswerI Limits in ρ ρ ∈ 0,2 I The function to integrate is f = ρ2 sin(φ)sin(θ) I = Z π 0 Z π/2 0 Z 2 0 ρ2 sin(φ)sin(θ) ρ2 sin(φ) dρ dφ dθ4 Abstract and Applied Analysis In this study, our goal is to prove dh(r)/dr0Sincein(25), both g(r)and var(cos2θ)/cos2θ2 are always positive, to achieve our goal, we only need to prove the two theorems below Theorem 21 Q 1(r)≡g(r)−1−2g(r)cos2θ2 0 (26) Theorem 22 Q 2(r)≡var(cos2θ)−1cos2θ 0 (27) Remark 23



Solved 81 X Dx Example 1 Evaluate X2 Solution Let X 9 Chegg Com



Pdf 3c3 Strategy Integra Stu Pdf Edith Castillo Academia Edu
2 cos2 θ cos 22 θ dθ 9 π Z π1 2 cos2θ cos4 θ 1 2dθ 9 π θ sin2θ sin4 θ 8 θ 2π 9π from AMATH 231 at University of WaterlooSee the answer Evaluate the integral1/2/19 · (sin2θ)^2=1/2 1/2cos4θ 所以得到 ∫ (sin2θ)^2 dθ =∫ 1/2 1/2cos4θ dθ =θ/2 1/8 *sin4θ 那么代入上下限2π和0, 得到定积分=π



The Cauchy Schwarz Inequality Manualzz



Doc Polar Curves Calculus 3 Polar Coordinates rhus Dc Academia Edu
Question Evaluate The Integral π/2 3 Cos2θ Dθ 0 This problem has been solved!Csc(x)^22=0 Add to both sides of the equation Take the root of both sides of the to eliminate the exponent on the left side The complete solution is the result of both the positive and negative portions of the solutionSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



Solved Evaluate The Integral Integrate Sin 11 Theta Cos Chegg Com


Solution Set Simple Harmonic Motion Physics 107
π 2 5 θ 5 π 2 に対応する曲線とy 軸で囲まれる部 分の面積を2倍したものになるよって S = 2· 1 2 ∫ π 2 − π 2 (1sinθ)2 dθ = ∫ π 2 − π 2 (12sinθ sin2 θ) dθ = θ −2cosθ π 2 − π 2 ∫ π 2 − π 2 sin2 θ dθ = π 2 ∫ π 2 0 sin2 θ dθ (* sin2 θ は偶関数) = π 2 ∫ π 2 0 1Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreCollect Math 47, 1 (1996), 1–21 c 1996 Universitat de Barcelona Range of the generalized Radon transform associated with partial differential operators M Mili Department of Mathematics, Faculty of Sciences of Monastir, Monastir 5019, Tunisia



Calculus Set Free Infinitesimals To The Rescue Volume 3 Spring 21 Preliminary Edition By Bryan Dawson Issuu


Math 550 Calculus Iii In Class Exercises


Double Integrals In Polar Coordinates Page 2



Weierstrass Substitution Wikipedia



If X A Cos 28 28 Sin 28 And Y A Sin 28 28 Cos 28 Find



Lab 4 And With Answers



Trigonometric Substitutions



Pdf Multiple Integrals Exercise Set 14 1 Guilherme Cousseau Cavion Academia Edu


Evaluate Sin8 Cos 58 D8 For 8 0 P 2 Sarthaks Econnect Largest Online Education Community


Integrating Cos 6 X Dx From 0 To Pi 2 Physics Forums


Find The Integral Of Math Int 0 Pi 2 Frac Dx 4 Cos 2x 9 Sin 2x Math Quora



Polar Curves Intersections Ppt Download



Resposta Do Capitulo 15



With Plots Ex11 P1 Plot Sqrt 4 Cos 2 Theta



Ex 6 2 9 Prove That Y 4 Sin 2 Cos Theta Is Increasing



Trigonometric Substitution Wikipedia



Evaluate The Integral P 47 9 Cos2 8 Cos2 8 D8 Youtube
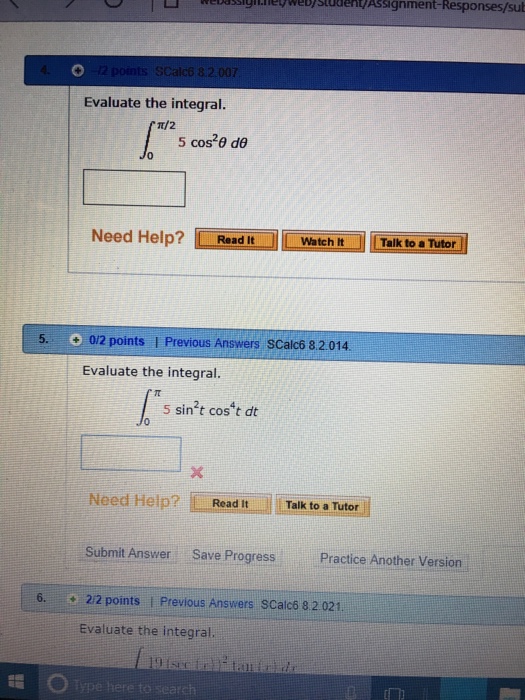


Solved Evaluate The Integral Integral 0 Pi 2 5 Cos 2 The Chegg Com


Solution Set Simple Harmonic Motion Physics 107



Problem 1 Think Of A Cone 45degrees Is Cut With A Horizontal



Ex 6 2 9 Prove That Y 4 Sin 2 Cos Theta Is Increasing


Math 550 Calculus Iii In Class Exercises


13 8 Chapter 8 Physics Libretexts



Int 0 Pi 4 1 Cos 2 Theta Cos 2 Theta D Theta Evaluate The Integral Youtube



Resposta Do Capitulo 15



Trigonometric Substitution Wikipedia



Trigonometric Integrals
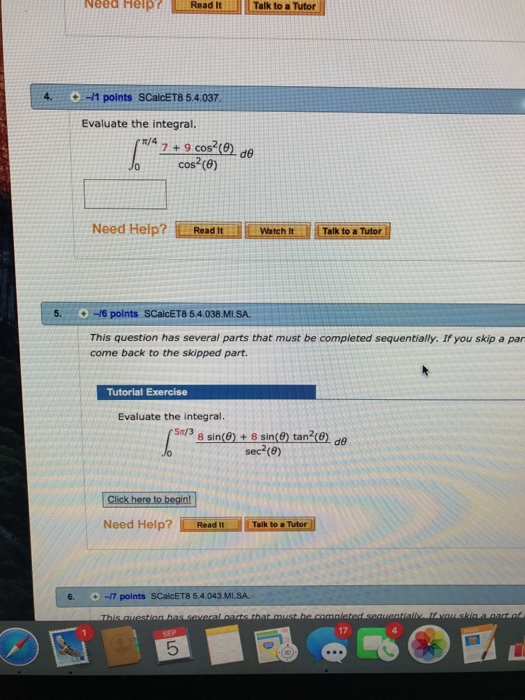


Solved Evaluate The Integral Integral Pi 4 0 7 9 Cos 2 Chegg Com



Q37 Integral Of Cos 2 Theta From 0 To Pi 2 Youtube



Techniques Of Integration


If P 2 A 2cos 28 B 2sin 28 Then Prove That P D 2p D8 2 A 2b 2 P 3 Sarthaks Econnect Largest Online Education Community


Integrating Cos 6 X Dx From 0 To Pi 2 Physics Forums



Ex 6 2 9 Prove That Y 4 Sin 2 Cos Theta Is Increasing



Asymptotic Velocity Of Relativistic E B Drift Aip Advances Vol 11 No 3



Fp3 Chapter 4 Integration Ppt Download



Trigonometric Substitution Wikipedia



Evaluate The Integral Cos 2 Theta D Theta Youtube



Chapter 10 Polar Coordinates Parametric Equations
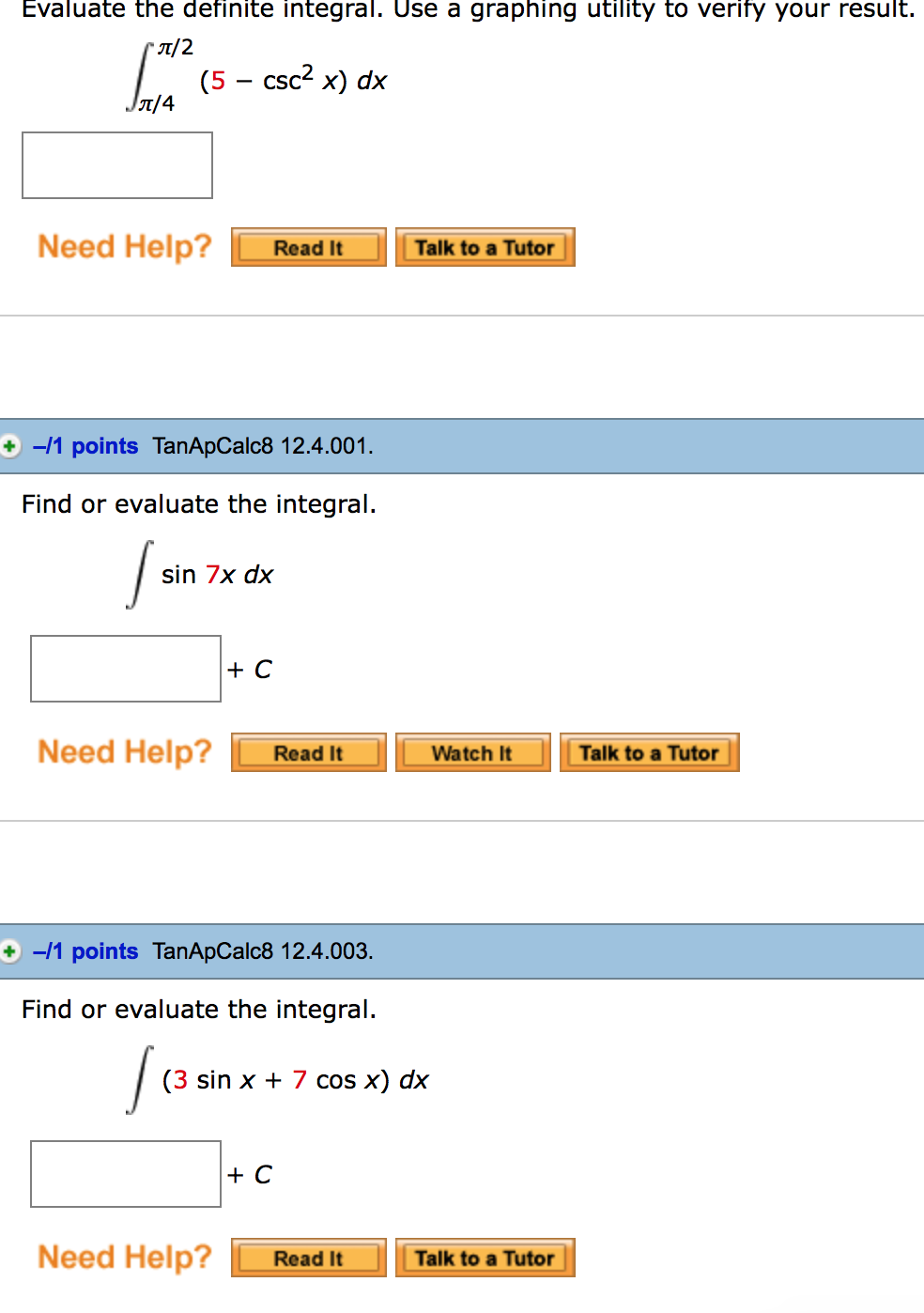


Solved Evaluate The Definite Integral Use A Graphing Uti Chegg Com



Solving Sinusoidal Equations Of The Form Sin X D Video Khan Academy



0 件のコメント:
コメントを投稿